置换的奇偶性 Parity of a permutation
在数学中,当X是一个至少有两个元素的有限集合时,X的置换(即从X到X的双射)可分为大小相同的两类:奇置换与偶置换。如果X固定了任何一个全序,X的一个置换 的奇偶性可以定义为
的奇偶性可以定义为 中反向对个数的奇偶性。所谓反向对即X中二元组
中反向对个数的奇偶性。所谓反向对即X中二元组 使得
使得 且
且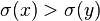 。这里
。这里 为置换
为置换 中第
中第 位的元素。
位的元素。
一个置换 的符号(sign或signature)记作sgn(σ):如果
的符号(sign或signature)记作sgn(σ):如果 是偶数则定义为 +1,如果
是偶数则定义为 +1,如果 是奇数则定义为 -1。符号定义了对称群Sn的交错特征。置换的符号另一个更一般的符号为列维-奇维塔符号(
是奇数则定义为 -1。符号定义了对称群Sn的交错特征。置换的符号另一个更一般的符号为列维-奇维塔符号( ),定义在X到X的所有映射上,而在非双射映射上取值为0。
),定义在X到X的所有映射上,而在非双射映射上取值为0。

 of X can be defined as the parity of the number of inversions for
of X can be defined as the parity of the number of inversions for .
.