小平消没定理
小平消没定理是复几何及代数几何中的重要结果,在复流形的分类问题(例如Enriques-Kodaira Classification)上扮演重要角色。
小平邦彦起初使用流形上的霍奇理论证明,当q>0
以上M 为任何紧致凯勒流形, 是M上的正规线丛,
是M上的正规线丛, 是正线丛。这个命题之后被推广为小平 中野消没定理:
是正线丛。这个命题之后被推广为小平 中野消没定理:
当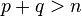 。
。 代表在L上的所有全纯 (p,0)-形式组成的层。
代表在L上的所有全纯 (p,0)-形式组成的层。
| 单词 | Kodaira vanishing theorem |
| 释义 |
Kodaira vanishing theorem
中文百科
小平消没定理小平消没定理是复几何及代数几何中的重要结果,在复流形的分类问题(例如Enriques-Kodaira Classification)上扮演重要角色。 小平邦彦起初使用流形上的霍奇理论证明,当q>0 以上M 为任何紧致凯勒流形, 当
英语百科
Kodaira vanishing theorem 小平消没定理In mathematics, the Kodaira vanishing theorem is a basic result of complex manifold theory and complex algebraic geometry, describing general conditions under which sheaf cohomology groups with indices q > 0 are automatically zero. The implications for the group with index q = 0 is usually that its dimension — the number of independent global sections — coincides with a holomorphic Euler characteristic that can be computed using the Hirzebruch-Riemann-Roch theorem. |
| 随便看 |
|
英汉网英语在线翻译词典收录了3779314条英语词汇在线翻译词条,基本涵盖了全部常用英语词汇的中英文双语翻译及用法,是英语学习的有利工具。