费马大定理 Fermat's Last Theorem
费马大定理,也称费马最后定理(法语:Le dernier théorème de Fermat),其概要为:
当正整数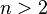 时,关于
时,关于 ,
,  ,
,  的不定方程
的不定方程
没有正整数解
以上陈述由17世纪法国数学家费马提出,一直被称为「费马猜想」,直到英国数学家安德鲁·怀尔斯(Andrew John Wiles)及其学生理查·泰勒(Richard Taylor)于1995年将他们的证明出版后,才称为「费马大定理」。这个猜想最初出现费马的《页边笔记》中。尽管费马同时表明他已找到一个绝妙的证明而页边没有足够的空位写下,但仍然经过数学家们三个多世纪的努力,猜想才变成了定理。在冲击这个数论世纪难题的过程中,无论是不完全的还是最后完整的证明,都给数学界带来很大的影响;很多的数学结果、甚至数学分支在这个过程中诞生了,包括代数几何中的椭圆曲线和模形式,以及伽罗瓦理论和赫克代数等。这也令人怀疑当初费马是否真的找到了正确证明。而安德鲁·怀尔斯由于成功证明此定理,获得了包括邵逸夫奖在内的数十个奖项。



